A very fast way of estimating a 2_log(x)
Often a Log Compression is used to create a good match of (detected) signals that contain a very high dynamic range to be able to become displayed on a Monitor/display (CRT, LCD, OLED) that has a significant lower dynamic range. Or a Log Compression maybe used to have a dB scale of a (detected) signal, for measurement purposes.
Here a very fast manner to estimate a logarithm is demonstated...
Log compressions are often utilized in displaying high dynamic signals, there might also be more signal-channels to be compressed concurrently.
In such an application it is needed to produce a logarithm fast like e.g. 5..10nSec (200, 100 Mhz)
When looking to a logarithm, we can make use of a very nice property.
It is this logarithm property and matching this with the fact that of digital numbers, the bits work in powers of two, that can be used to produce a logarithm in a fast manner.
The mathematica magicians figured out the relation: 2_log(x) = 10_log(x) / 10_log(2) so 10_log(x) = 10_log(2) * 2_log(x) so the dBval(Usignal) = 20 * 10_log(Usignal) = 20 * 10_log(2) * 2_log(Usignal) = 6.0205999 * 2_log(Usignal).
6.0205999 is the famous 6dB increase of digital dynamic range, per adding 1 bit.
The fastest way to 'compute' a log() is just to have a lookup-table, with in the table precomputed results stored. But the problem is that would need a very large lookuptable.., suppose a digital Usignal is represented with 16-bits then it needs a 64K long table. That is long, but might be manageable. But what if the input signal is a (Power)Psignal (e.g. that was derived from a Usignal) than the number of bits might be 32-bits. then the table length 4Giga-values is not practical anymore.. But fortunately, the smart mathematica magicians learned us more..
In the past history there where Logarithm tables, used , and prior to the calculators, slide rulers where used, the scales where based on a logarithm. This was used to perform multiplications in a 'fast' manner with shifting two log-scales, it was based on log(A * B) = log(A) + log(B).
A important property of the Logarithm that will help us to minimize a lookup table is.... You can split a Logarithm in Exponent(integer) and mval(float), with using: 2_log( x ) = 2_log( 2^exp * (x/(2^exp)) ) = 2_log( 2^exp ) + 2_log( x/(2^exp) )
As an example: 20358 => 0000 0000 0100 1111 1000 0110
just look at the position of the most left 1 (note: must use a unsigned value)
that is at bit 14...., so we already found the Exp=14. And now the bits below the most left '1' is ---- ---- -(1)00 1111 1000 0110 and now just shift the bits according to 20358 >> 14 = 1.24255371
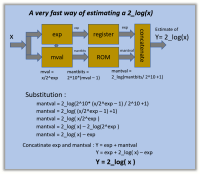
Figure 1 (LogPrinciple.png) gives an overview of the system that can be used to find a 2_log(x) in a very fast manner. The substitution shows in a nice way how it is build up, to have this contraption to actualy produce a 2_log(x)
Figure 2 (GenerateTable.png) shows python code that generates the ROM-table content
Figure 3 (Usage.png) shows a python code example how to extract the 2_log(x),
but here the exp is extracted via a 2_log() computation.., should replace that by finding the bit position of the most significant bit with the value '1'. The python code it is not writen to be fast, it just serves to show the equivalent manner how the cicuit of Fig_1 procedes to extract the 2_log(x)



Discussion (0 comments)